[ 의료영상 ] Medical Image Segmentation (4.Graph Cut Method)
MOOC 강좌 '컴퓨터비전, 머신러닝, 딥러닝을 이용한 의료영상분석' 강의를 리뷰 및 정리한 게시물입니다.

Graph Cut Method를 이용하여 Segmentation Task를 진행할 때는 이미지를 Graph Model로 정의하고, Graph의 Label을 정의하는 문제로 생각한다.

우측 이미지의 검은색이 background, 흰색이 foreground라고 가정한다. Graph Model에서는 관찰된 영상의 color 값을 obsevation이라 한다. 푸른색과 보라색을 따로 분할한다고 하면 푸른색을 0, 보라색을 1이라고 지정해야 한다. (Labeling)
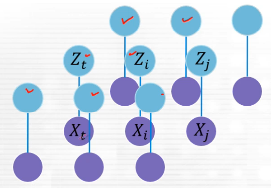
해당 이미지를 그래프화 한 그림이 우측 그림의 상단부이고,
우리가 구하고 싶은 것은 X값들이다. 이는 P(X1 ~ X9ㅣZ1 ~ Z9) 라는 Posterior Probability를 통해 구할 수 있다. 이를 계산하는 식은 베이즈 정리를 통해 계산되고 그 과정은 아래 그림과 같다.

Z값들이 다 관찰이 되었을 때, X값을 찾는 것이 어려우니 베이즈 정리를 활용하는 것이다.
분모는 관찰되는 값들이고, 분자에서 P(Z1 ~ Z9 ㅣX1 ~ X9)라는 Likelihood Probability와 P(X1 ~ X9)라는 Prior Probability 의 곱으로 나타난다.
정리하면 Posterior Probability를 직접 푸는 것이 아니라 Likelihood Prob과 Prior Prob에 비례함을 이용한다는 것이다.
이때, Likelihood Prob만 봐도 X1 ~ X9라는 모든 조합에 대하여 확률값을 구해야하므로 이 상황에서는 계산이 어렵다. 따라서 하나의 가정이 더 추가되어야 한다. -> Naive Assumption
각 sample들이 독립이라는 가정이다. 이를 통해 Likelihood Prob Term은 P(Z1ㅣX1) ~ P(Z9ㅣX9)의 곱으로 표현할 수 있다. 사실 이 가정이 이미 전제에 깔린 그림이 위 Graph Figure다. 그렇다면 Naive Assumption가 가지는 의미를 수식으로 이해해보자.

이미지의 (2,1) 부분을 Labeling한다고 생각해보면 검은색이 0, 흰색이 1이라고 Labeling 되어있는 상황에서 우측 수식의 아래 식 2가지를 계산하면 그 결과가 어떨까?
a) P(Z(2,1)=옅은 푸른색ㅣX(2,1)=0)
b) P(Z(2,1)=옅은 푸른색ㅣX(2,1)=1)
옅은 푸른색은 0과 더 가깝기 때문에 a) 식이 b) 식보다 더 클 것이다.
즉, Likelihood Term의 정의는 픽셀값 하나하나와 Label 값의 유사도를 나타내는 것이다. 그리고 확률값을 정의할 때 다른 픽셀을 고려하지 않겠다는 것이 Naive Assumption으로 들어가는 것이다.

Medical Image를 예시로 들어보자. foreground가 spine이라면 foreground는 상당히 밝은 영역이다. 그렇기에 외곽을 포함하여 밝은 부분들과 중간중간 Noise들도 foreground로 labeling 될 것이다. 이러한 문제를 해결해주는 것이 수식에서 Prior Probability에 해당한다.
P(X1=0, X2=0, ... , X8=0, X9=0) = ?
P(X1=0, X2=0, ... , X8=0, X9=1) = ?
P(X1=0, X2=0, ... , X8=1, X9=0) = ?
...
Likelihood Prob과 Prior Prob의 곱이 최대가 되는 X들을 찾아주는 것이 최종적인 목표임을 잊지 말자.
Prior Prob을 계산하기 위해 다양한 Label 조합에 의한 확률값을 계산한다. 계산이 복잡함을 알 수 있다. 여기서도 또 다른 가정을 해주는데 X1의 Label을 확인할 때는 X2, X4처럼 주변의 Label과의 관계를 고려하겠다는 Markov Random Field 개념이 추가된다.

기존에 봤던 Naive Assumption이 좌측 구조이고, 우측이 Markov Random Field를 나타낸 것이다. 주변 Label들과의 관계도 고려한다면 어떤 일이 생길까?
(2,2)인 Zi 주변은 전부 보라색인데 혼자 파란색이라면 이미지의 관점에서 볼 때, Segmentation하고 싶은 부분의 Hole로 작용할 것이다. 하지만 Markov Random Field가 추가되면 (2,2) 역시 주변 보라색 Label의 영향을 받아 보라색으로 Labeling 될 확률이 높아진다는 것이다.
즉 Prior Term이 존재함으로써 Likelihood Prob을 높이면서 Prior Prob Term도 높인다는 것은 Label 사이의 경계 역시 어느정도 Smooth 해야 한다는 것이다.
실제 영상에서 확률을 어떻게 정의하고 모델을 어떻게 최적화 할 수 있는지는 To be continued.