모든 게시물은 macOS Monterey 12.0.1 버전 기준으로 작성하였습니다.
'이것이 취업을 위한 코딩 테스트다 with 파이썬' 토대로 작성하였습니다.
< 복습 >
- for문 쓸 때 무조건 for i in range() 가지 말고 리스트 그대로 iteration 할까도 고려하자.
- if l[i] == 0 or 1 으로 조건문 걸면 False or True로 인식해서 다 참으로 간다.(그런듯?)
- ㅣ = [] 형태로 리스트 초기화 후 for문에 l[i] 인덱싱하면 out of index 나온다.
- 리스트 sorting 할 때 l = l.sort() 하면 값 없어진다. 그냥 l.sort() 써라.
- 리스트 크기를 size(l)로 구할 수 없다. len(l)로 구해라.
- 그래프 모델링 할 때는 노드 인덱싱과 맞추기 위해 그래프의 첫 리스트를 []로 초기화한다.
- DFS는 재귀 함수 형태로 해결하고, BFS는 while queue로 반복문을 건다.
- BFS는 방문 처리하기 전에 popleft로 원소를 빼주고, 방문처리하면 append 잊지 말자.
순차 탐색 알고리즘
리스트 데이터를 매우 빠르게 탐색하는 이진 탐색 알고리즘에 대해서 공부하기 전에
가장 기본 탐색 방법인 순차 탐색에 대해 먼저 이해할 필요가 있다.
순차 탐색에서는 리스트의 특정한 데이터를 찾기 위해 앞에서부터 하나씩 확인한다.
순차 탐색을 파이썬 코드로 작성하면 다음과 같다.

순차 탐색은 데이터 정렬 여부와 상관없이 가장 앞에 있는 원소부터 하나씩 확인하니
데이터의 개수가 N일 때 최대 N번의 비교연산이 필요하므로 최악의 경우 O(N)이다.
이진 탐색 알고리즘
이진 탐색은 배열 내부의 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다.
이진 탐색은 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 특징이 있다.
이진 탐색은 위치를 나타내는 변수 3개를 사용하는데
탐색 범위의 시작점, 끝점, 그리고 중간점이 그것이다.




절반씩 데이터를 줄어들도록 만든다는 점은 앞서 다룬 퀵 정렬과 공통점이 있다.
구현하는 방법에는 재귀 함수를 이용하는 방법과 반복문을 이용하는 방법이 있다.
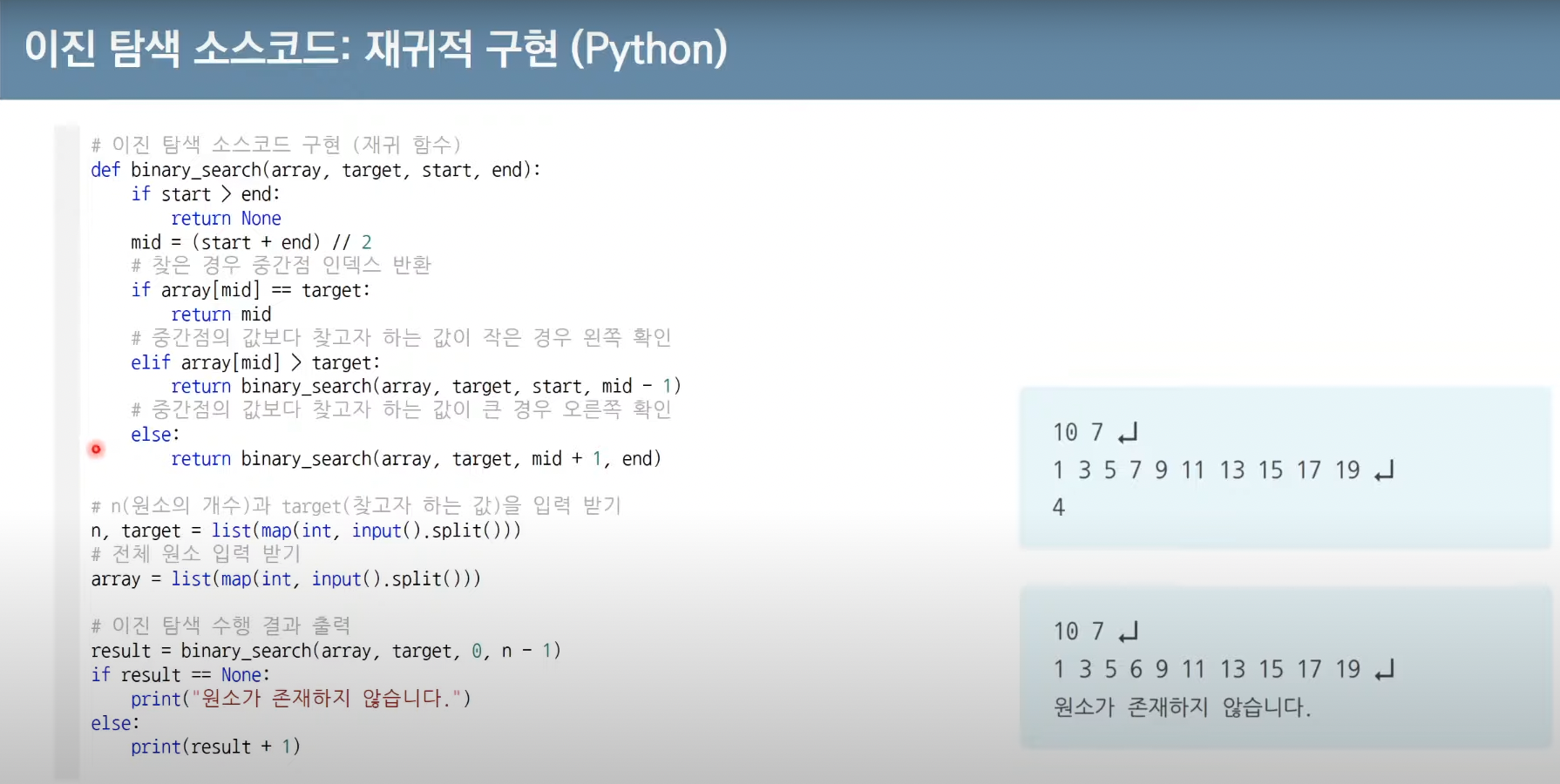
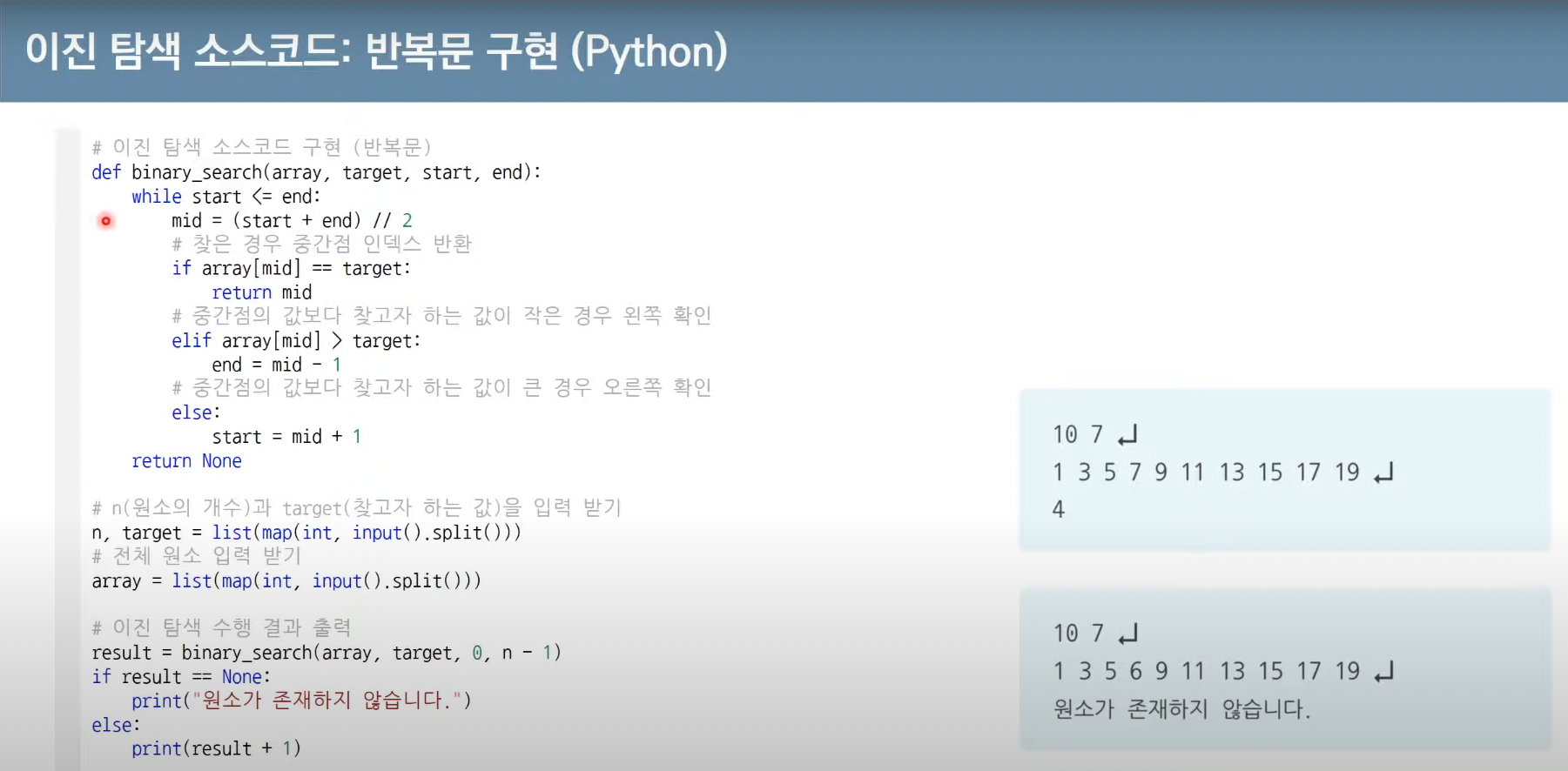
단순히 위 코드를 보면 이진 탐색이 단순하다고 느낄 수 있지만, 정작 참고할 코드가
없는 상태에서 이진 탐색 소스코드를 구현하는 것은 상당히 어려울 수 있다.
코드가 짧으니 이진 탐색을 처음 접한다면 여러번 입력하여 외우길 추천하고 있다.
코딩 테스트에서도 단골로 출제되는 문제이니 가급적 외우길 권한다고 한다.
연습 !
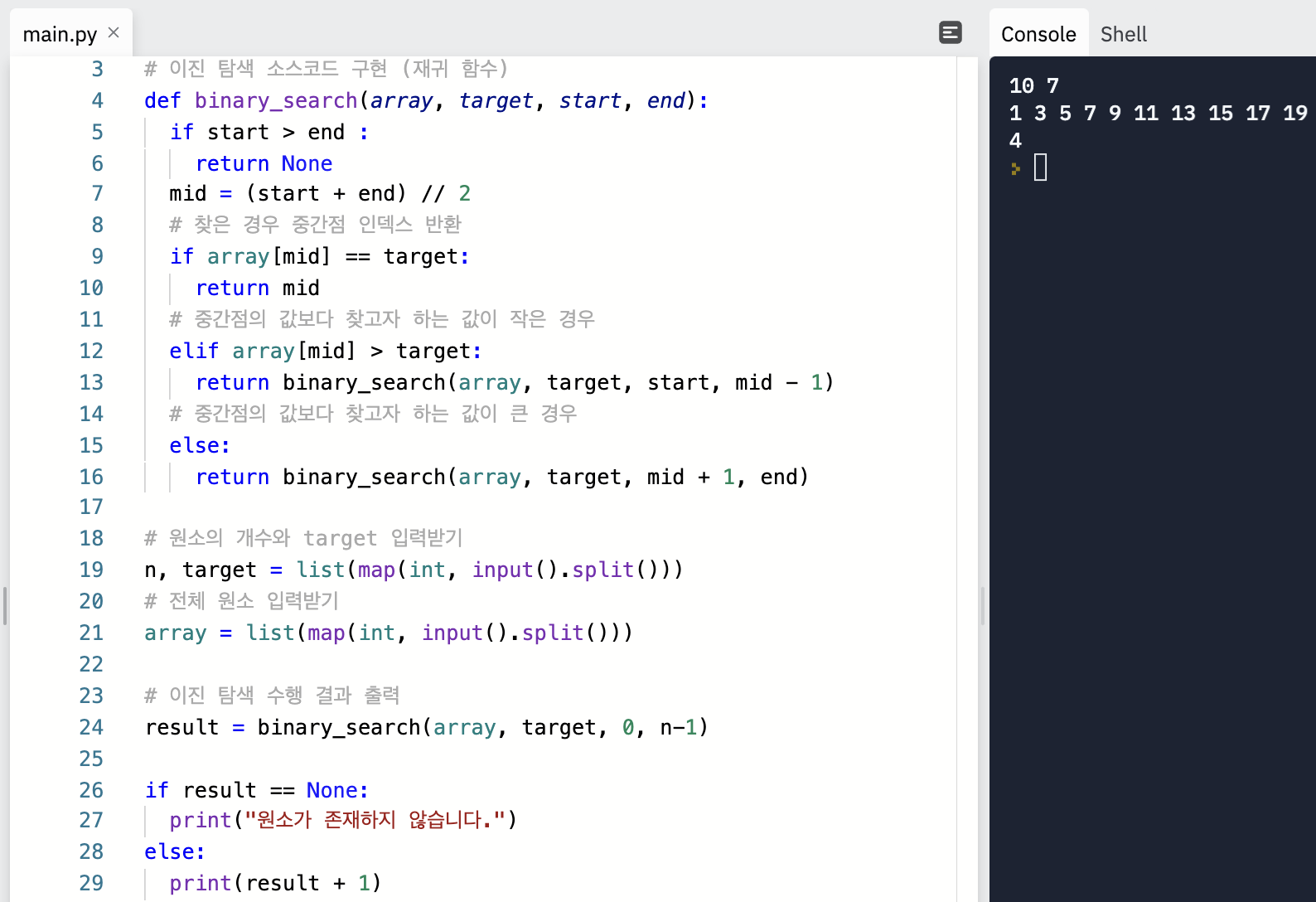
추가적으로 코딩 테스트 문제 풀이를 위해 알아두면 좋은 라이브러리가 있다.
이진 탐색 라이브러리로 값이 아닌 인덱스를 반환함에 주의하자.

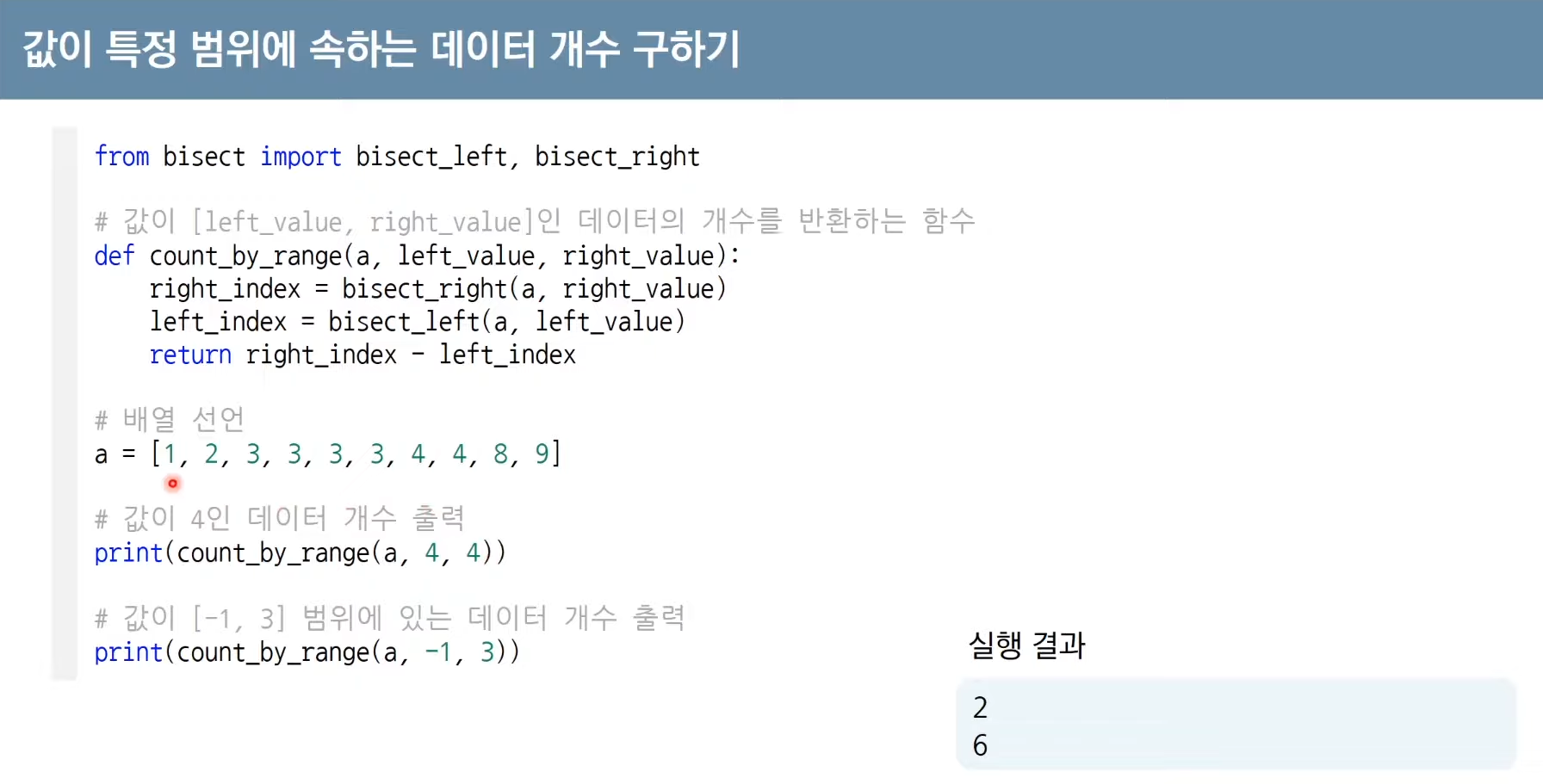
위를 이용하여 값이 특정 범위에 속하는 데이터 개수를 구할 수 있다.
뭔가 이미 이거 쓰면 풀릴 문제를 본 것 같기도 한데... 익혀두자.

실제로 이진 탐색을 활용해야 하는 문제들은 파라메트릭 서치 유형으로 출제된다.
여기서 최적화 문제란 어떤 함수의 값을 최대한 낮추거나 높이는 문제를 말한다.
이를 한번에 해결하기 어려우면 여러번의 결정 문제로 나누어 해결하는 기법이다.
문제 풀이 파트에서 알아보자.

이진 탐색 알고리즘 코딩 테스트 연습문제
떡볶이 떡 만들기


최적화 문제를 결정 문제로 바꿔 해결하는 Parametric Search 문제다.
조건의 만족 여부에 따라 그 탐색 범위를 좁혀 해결할 수 있다. 물론 못 풀었다..
우리가 절단기 높이를 키우면 잘린 떡의 길이는 줄어들 것이고,
절단기 높이를 낮추면 잘린 떡의 길이는 늘어날 것이니 이진 탐색 가능하단다.
즉, n만큼의 길이를 얻을 수 없다면 절단기 높이를 낮추면 되는 것이다.
또, 절단기 높이가 0부터 10억까지의 큰 탐색 범위를 가지니 이진 탐색을 떠올린다!
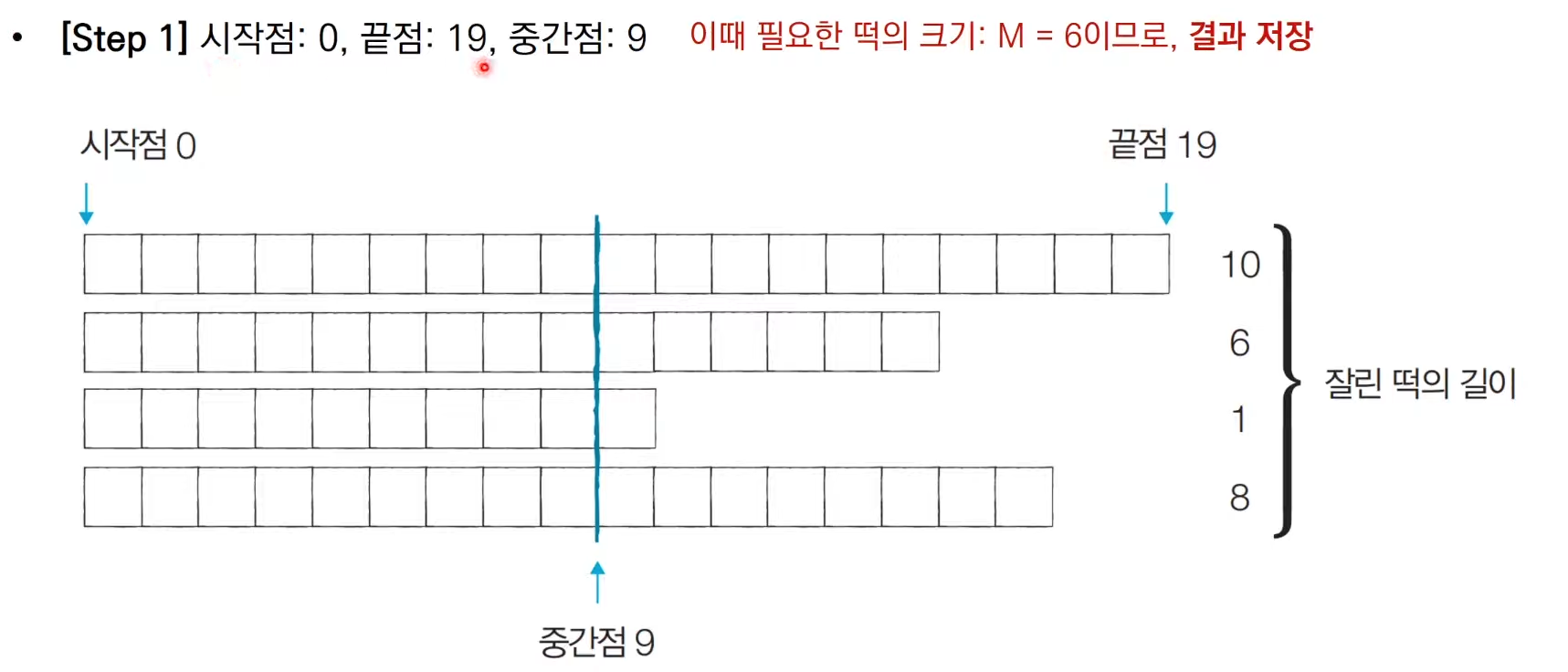
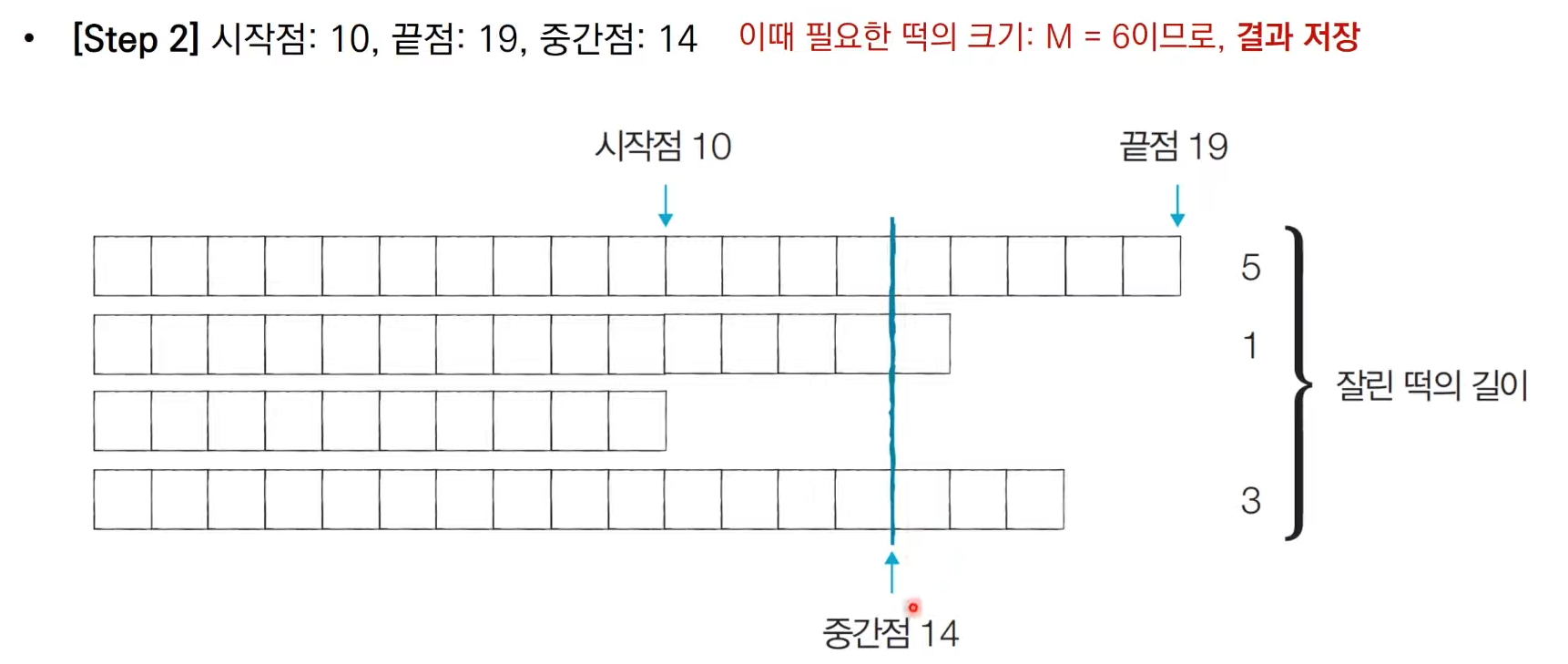
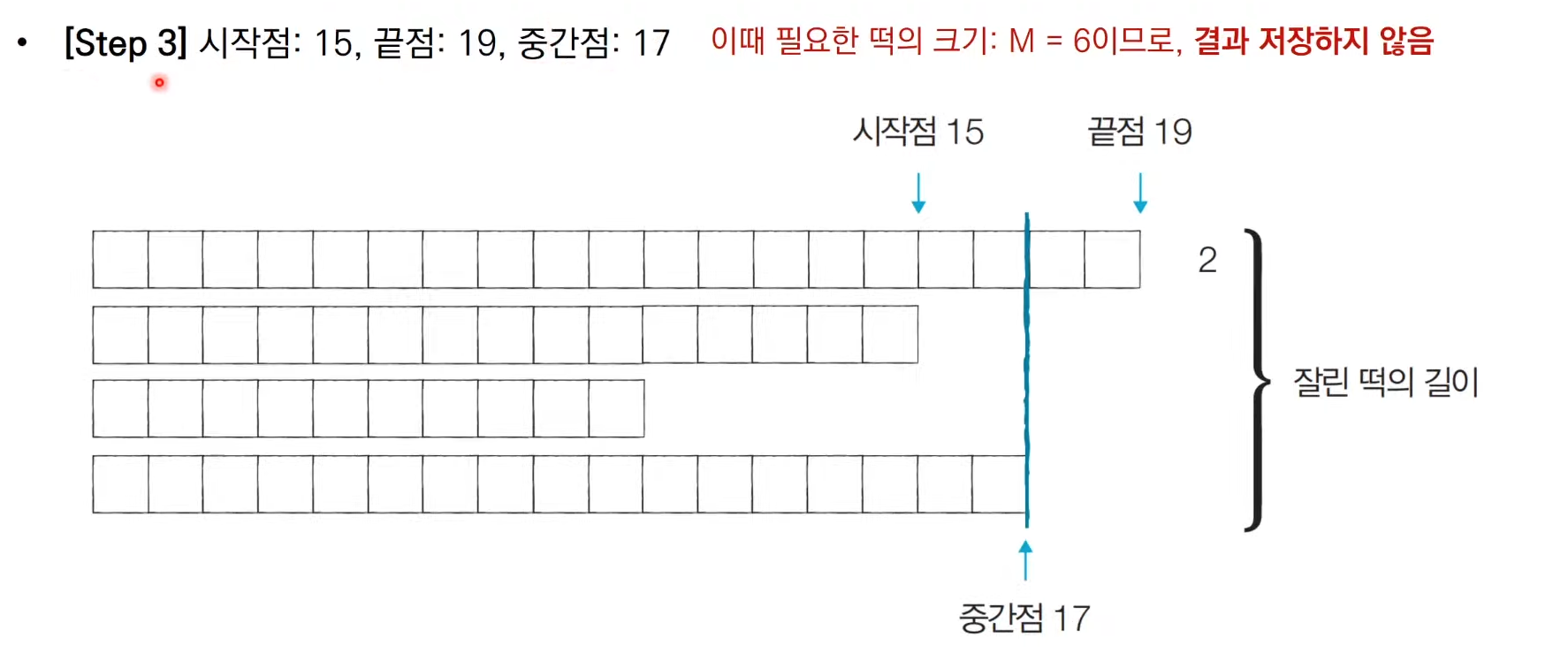
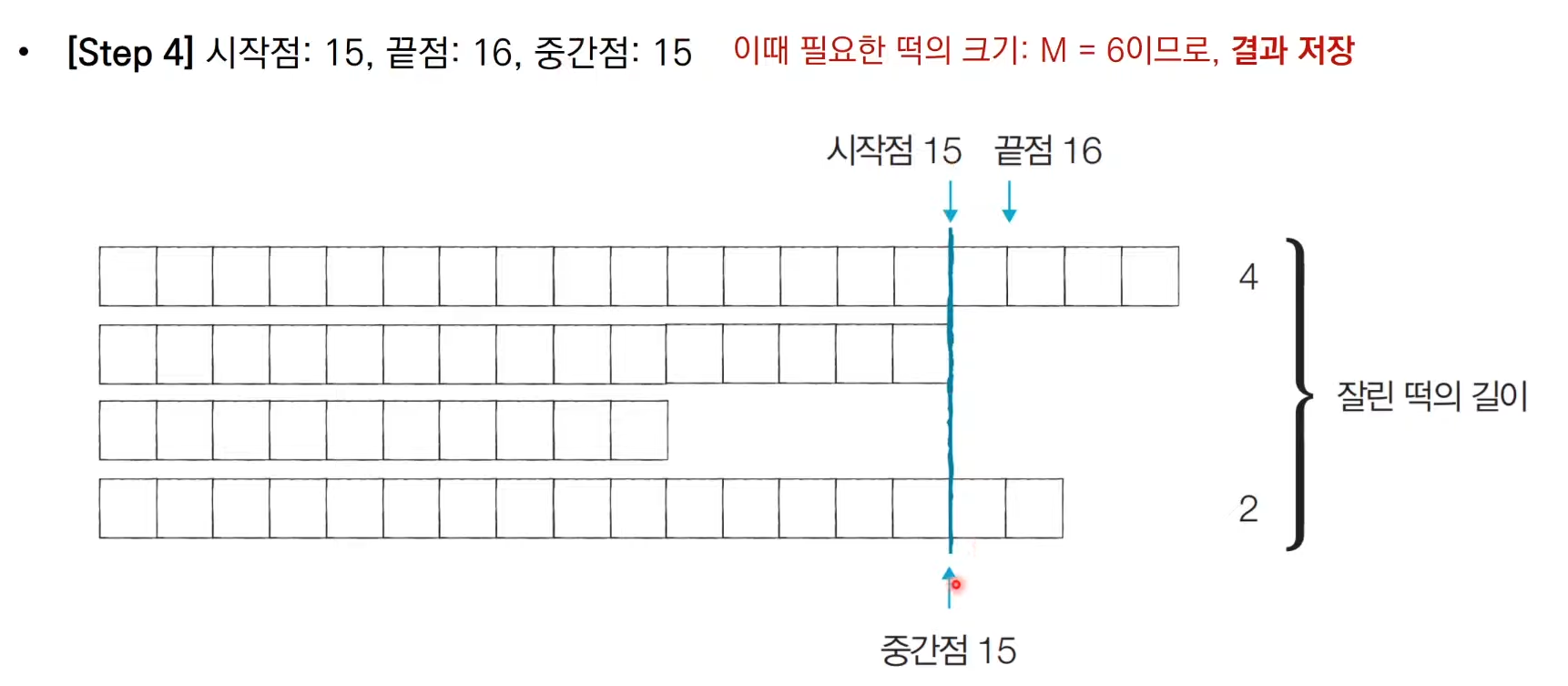
진짜 쉽지 않다..

또한 이 문제에서는 현재 얻을 수 있는 떡볶이의 양에 따라서 자를 위치를 결정하므로
이를 재귀적으로 구현하는 것은 귀찮은 작업이 될 수 있다. 따라서 이와 같은
파라메트릭 서치 문제 유형은 이진 탐색을 재귀적으로 구현하지 않고
반복문을 이용해 구현하면 더 간결하게 문제를 풀 수 있다.
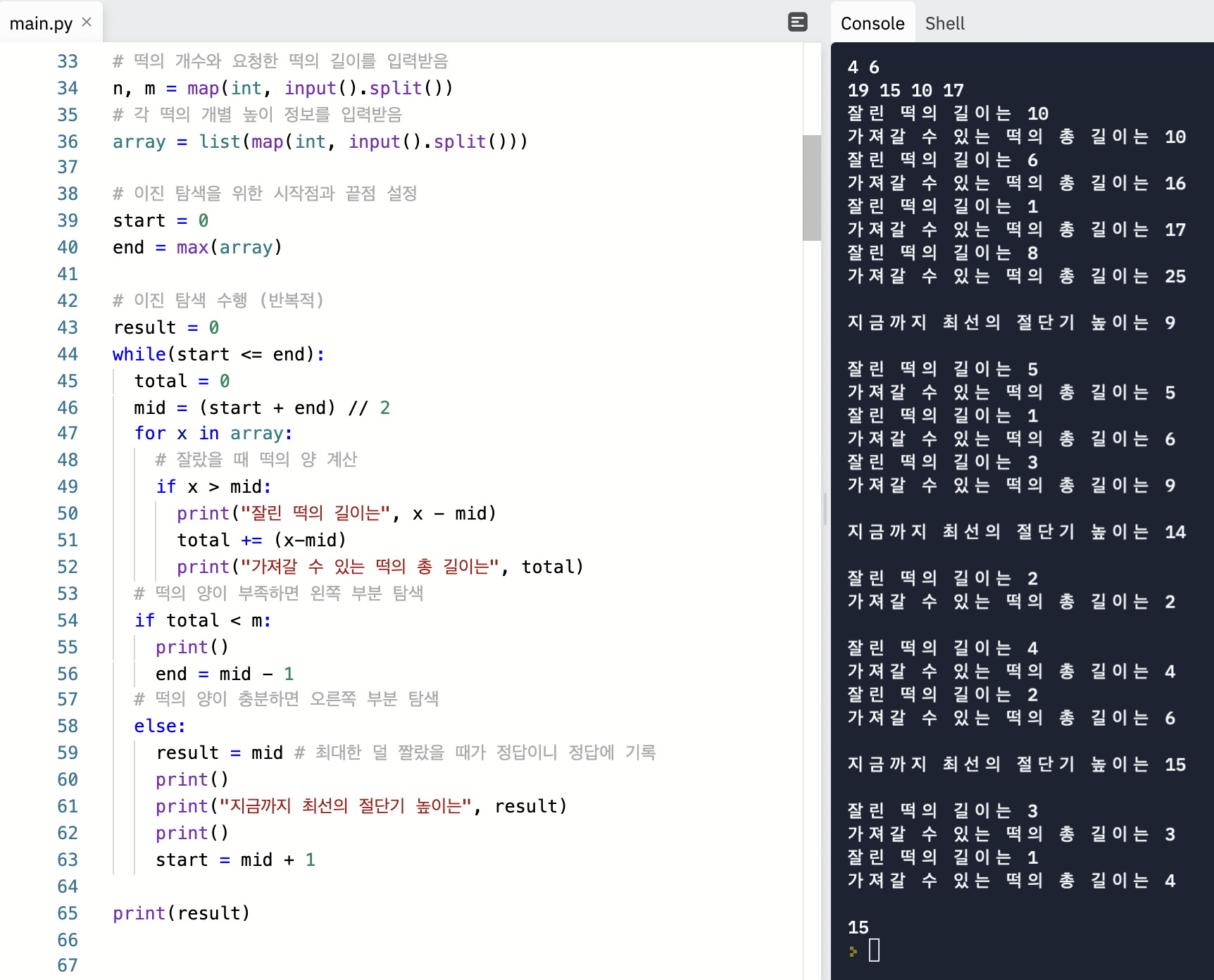
이진 탐색 알고리즘 코딩 테스트 연습문제
정렬된 배열에서 특정 수의 개수 구하기



원소들이 모두 정렬되어 있기에 수열 내에 x가 처음 등장하는 인덱스와
마지막으로 등장하는 인덱스를 계산한 뒤에 그 차이를 통해 문제를 해결할 수 있다.
하나는 데이터가 존재한다면 가장 첫 번째 위치를 찾는 이진 탐색 함수이며,
다른 하나는 데이터가 존재한다면 가장 마지막 위치를 찾는 이진 탐색 함수이다.
이 2개를 각각 실행한 뒤에 답을 도출하는 고난이도 문제의 테크닉이다.
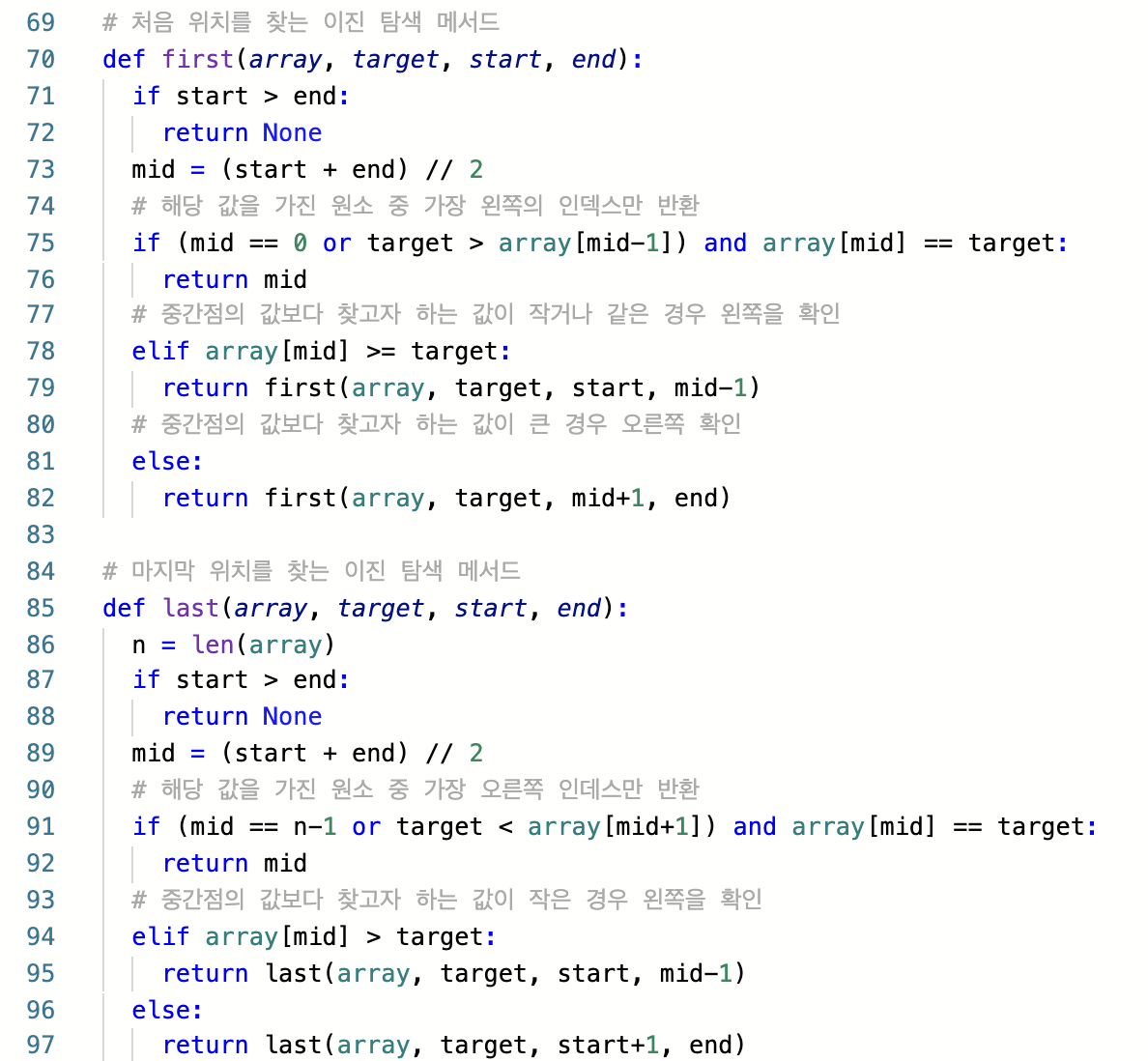
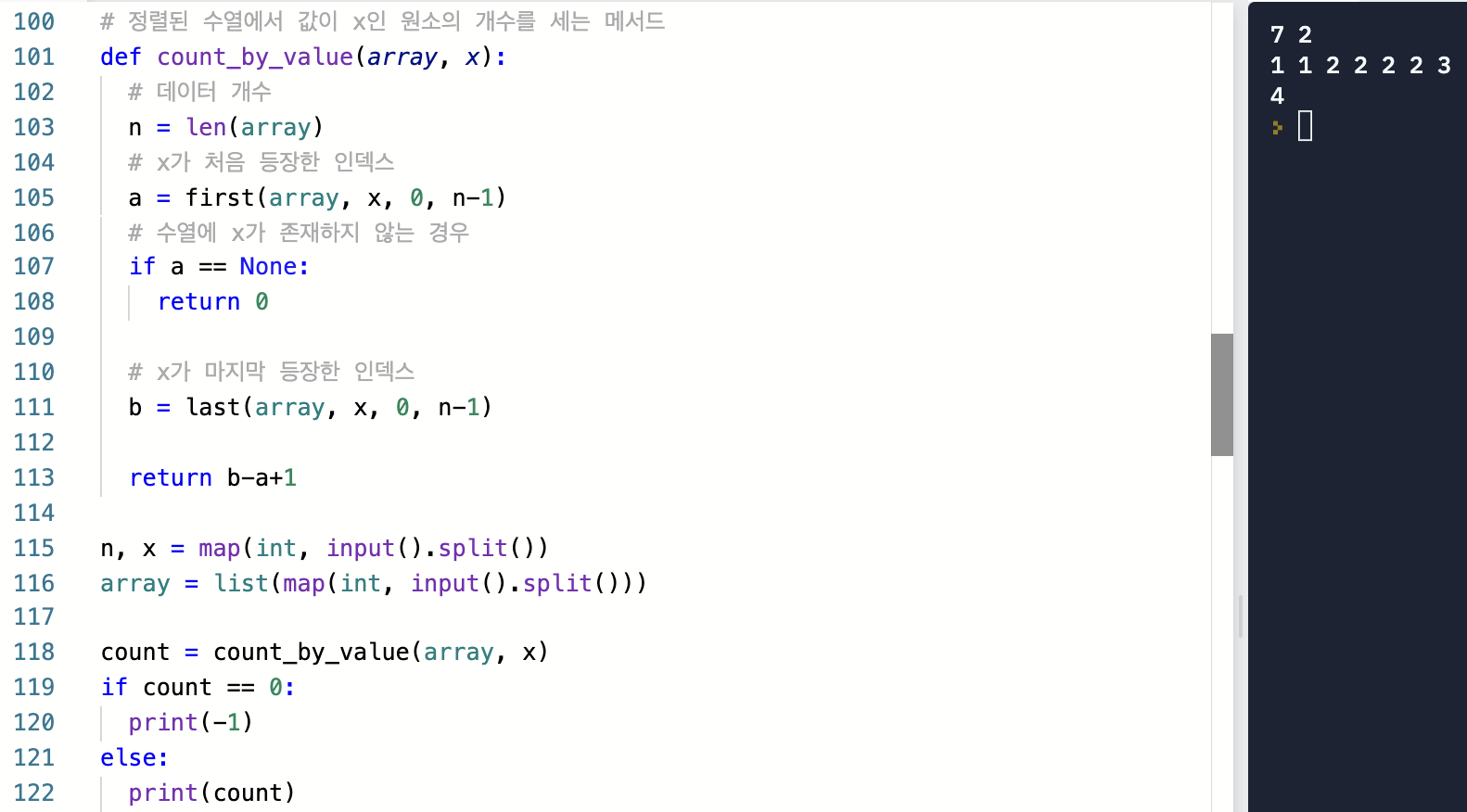
또한 이 문제는 단순히 정렬된 수열에서 특정한 값을 가지는 원소 개수를 구하므로
파이썬의 이진 탐색 라이브러리인 bisect를 적절히 활용하면 손쉽게 해결 가능하다.

'Python > 이코테 with 파이썬 정리' 카테고리의 다른 글
| [211221] 코딩 테스트를 위한 투 포인터 알고리즘 (0) | 2021.12.21 |
|---|---|
| [211217] 코딩 테스트를 위한 정렬 알고리즘 ( 선택 정렬, 삽입 정렬, 퀵 정렬, 계수 정렬 ) (0) | 2021.12.17 |
| [211216] 코딩 테스트를 위한 깊이 우선 탐색, 너비 우선 탐색 ( DFS & BFS ) (0) | 2021.12.16 |
| [211210] 코딩 테스트를 위한 그리디 알고리즘 ( Greedy Algorithms ) (0) | 2021.12.10 |
| [211203] 코딩 테스트를 위한 파이썬 표준 라이브러리 (0) | 2021.12.03 |