모든 게시물은 macOS Monterey 12.0.1 버전 기준으로 작성하였습니다.
부스트캠프 AI Tech 3기를 위한 Pre-Course 를 토대로 작성하였습니다.


Neural Network
생물학적 뇌의 신경망을 모방한 Computing System.
이미지라는 텐서가 주어지면 라벨이라는 벡터가 산출되는 모델이 있다고 하자.
내가 정의한 함수(행렬 연산과 비선형 연산의 반복)로 이를 근사하겠다.

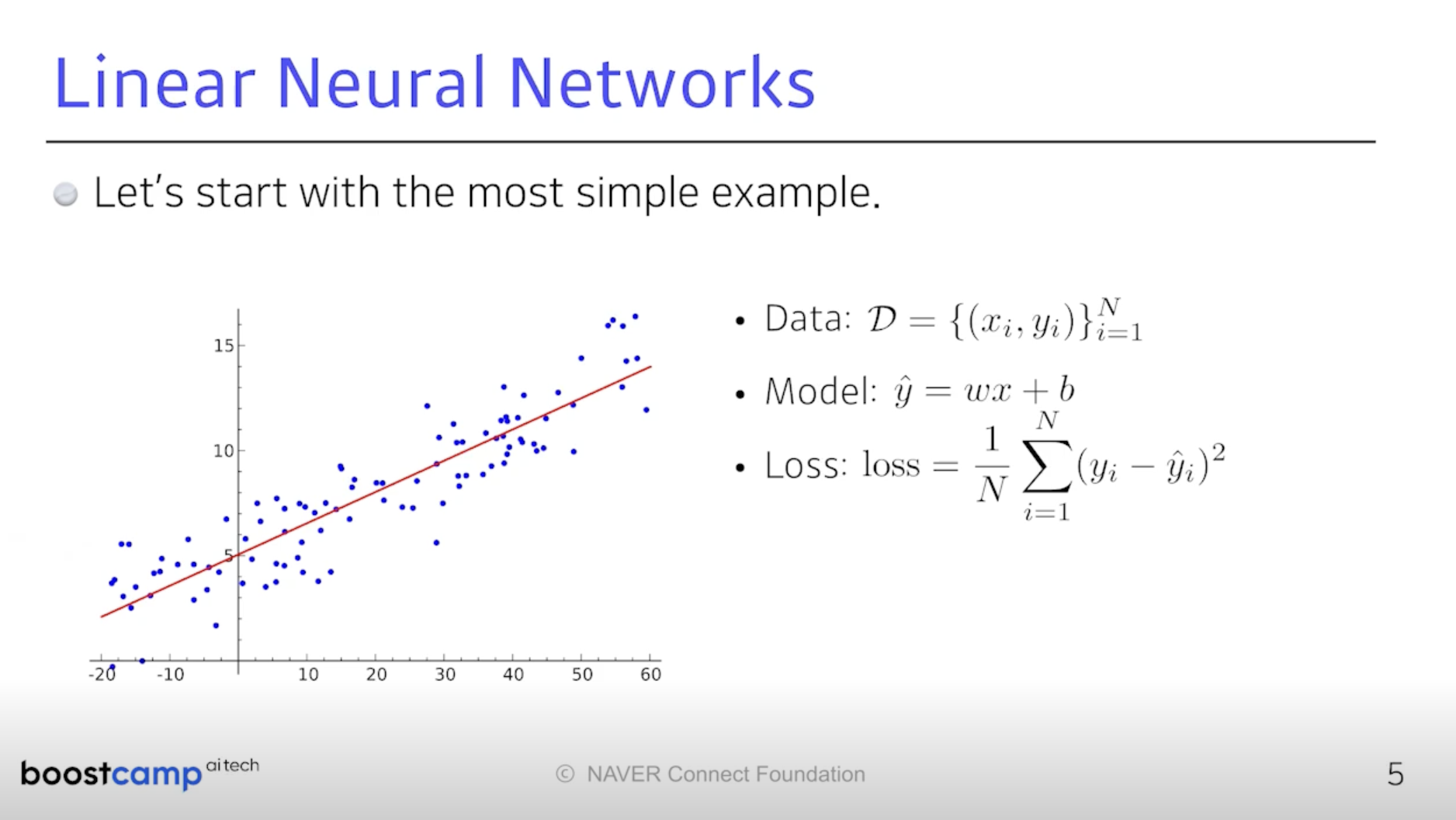
입력과 출력이 1차원인 문제가 있다고 하자. 선형회귀.
그 목적은 입력과 출력을 연결하는 모델을 찾는 것이다.
선형이므로 라인에 대한 기울기와 y절편 두 파라미터를 찾는 문제가 될 것이다.
데이터는 1차원 x와 y가 N개 모여있다. x에서 y_hat으로 mapping 시키는 선형모델
그 기울기와 절편을 찾는 것이 목표다. 이 목표에 가까워지면 그 값이 작아지는
Loss를 정의하고 이를 점차적으로 줄이겠다는 것이다. 여기서는 MSE.
어떻게 기울기와 절편을 찾을수 있을까?
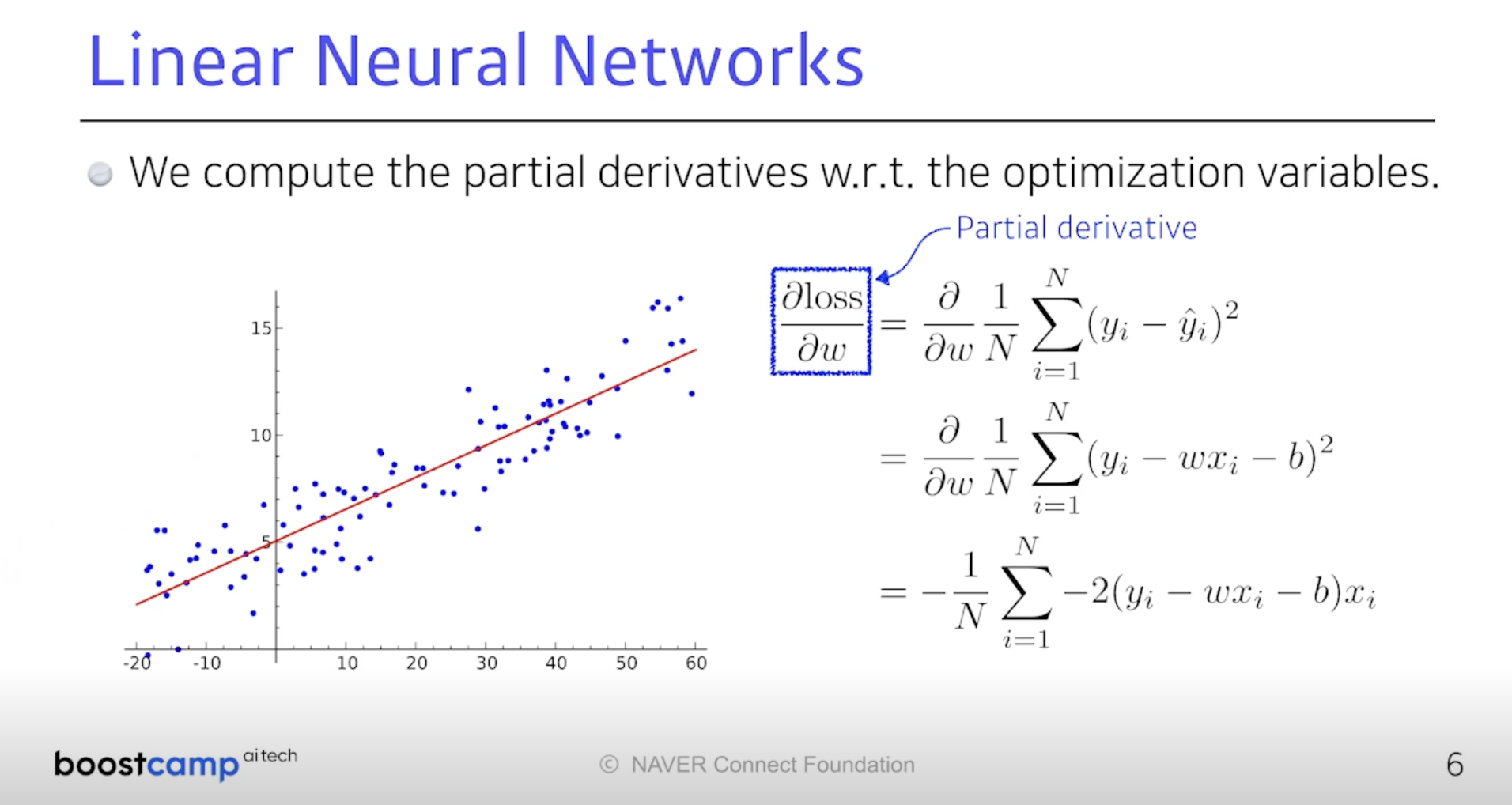
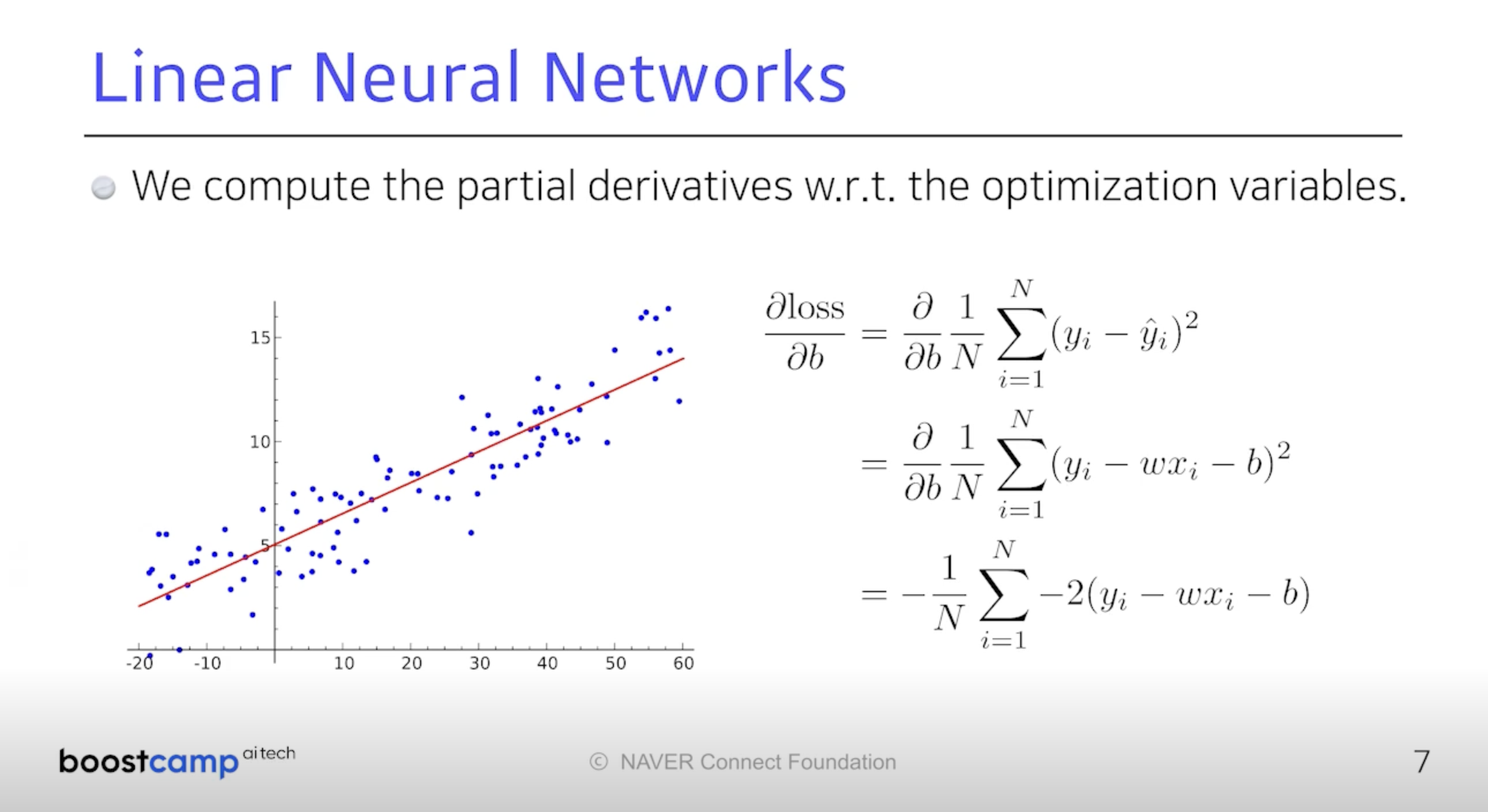
우리의 전략은 Back Propagation. 결국 Loss Function을 줄이면 되니까
나의 Parameter가 어느 방향으로 움직여야 Loss Function이 줄어드는지 보자.
Loss를 나의 각 Parameter로 미분하게 되는 방향의 역방향으로 Parameter를
갱신하다보면 Loss가 최저가 되는 순간이 올 것이고, 그것이 Optimal Parameters.
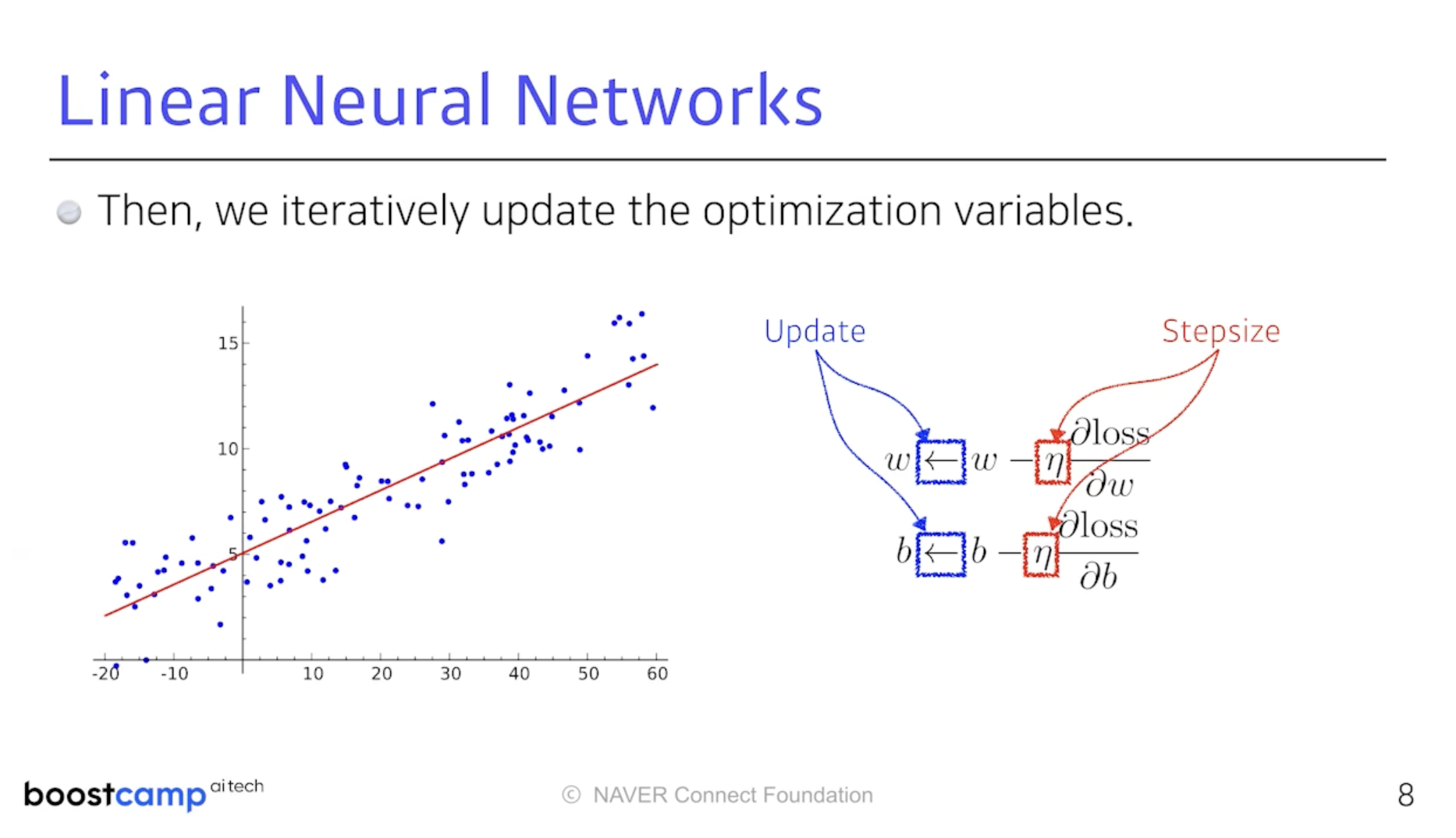
그 편미분 값들을 특정 step size를 곱한 값을 빼주는 방식으로 변수를 갱신한다.
이 방법을 Gradient Descent Method라 부른다. 주어진 Loss Function에 대해
편미분을 구하고 그 값을 빼줌으로써 최소값을 찾아간다는 것이다.

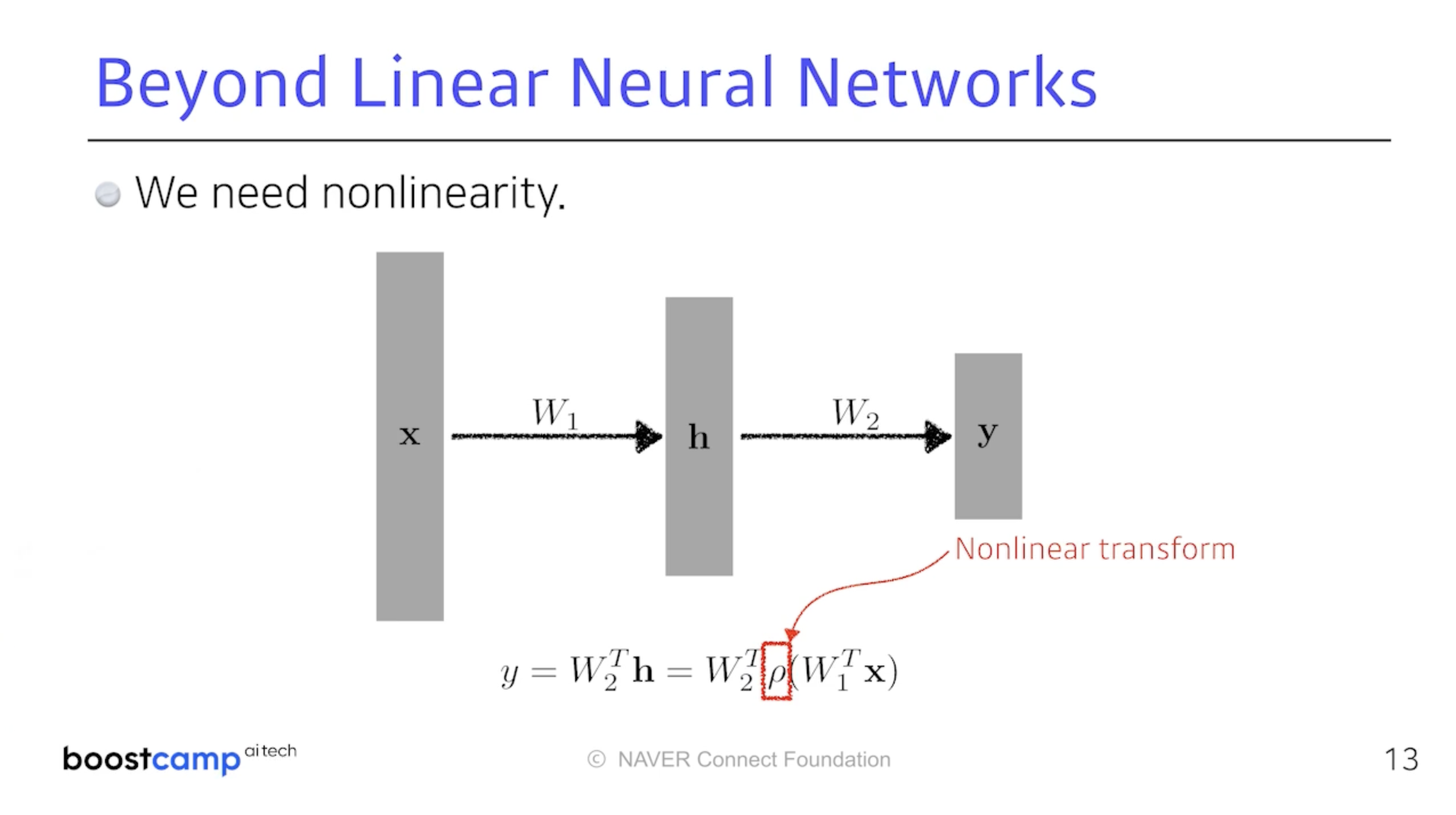
왼쪽의 사진처럼 이것을 단순히 쌓는다고 해봤자 행렬 두 개의 곱일 뿐이다.
이때 필요한 것이 바로 중간에 Non-linear Transform이다.
입력에서 출력까지 가는 Mapping의 표현 능력을 극대화 한다는 것이다.
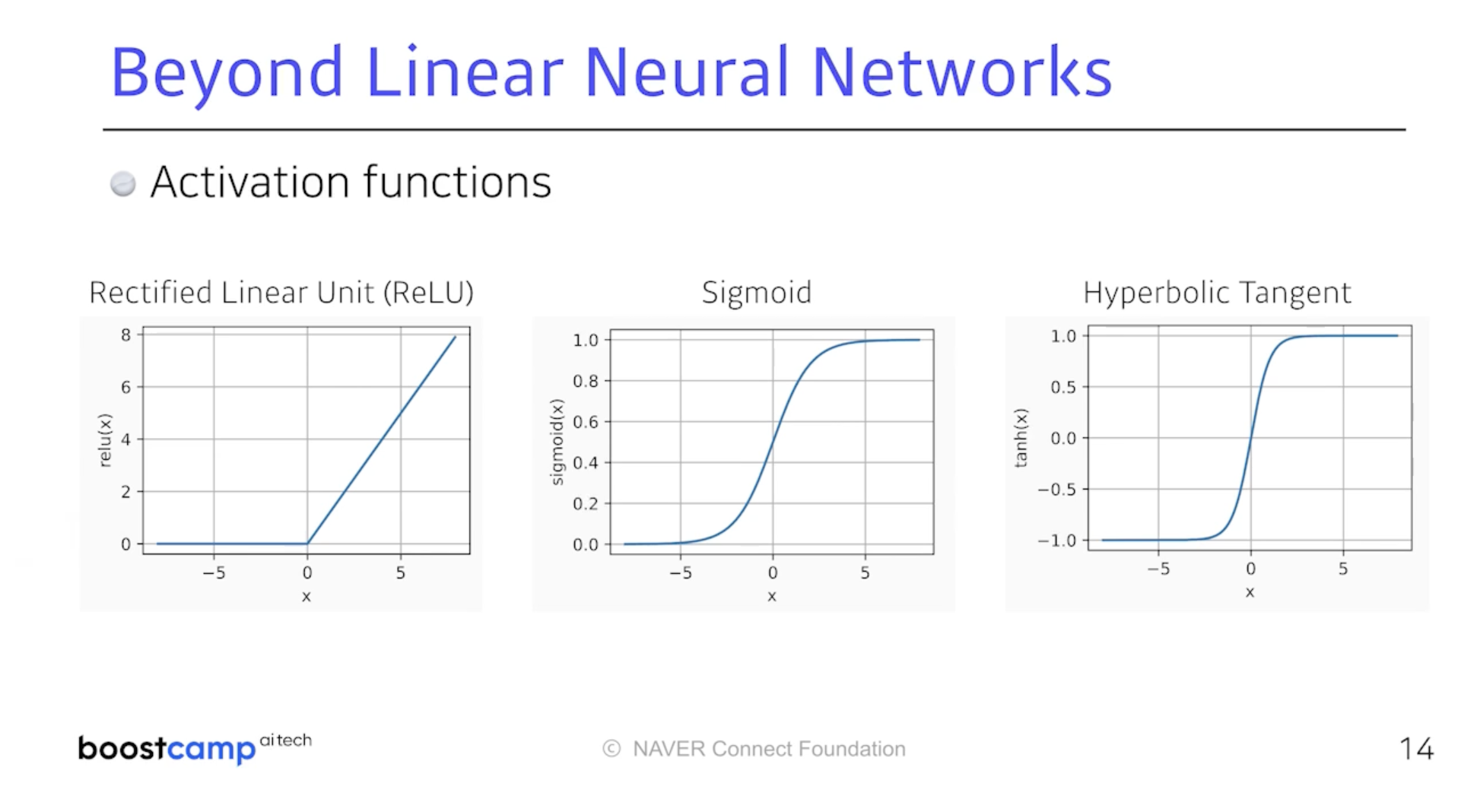
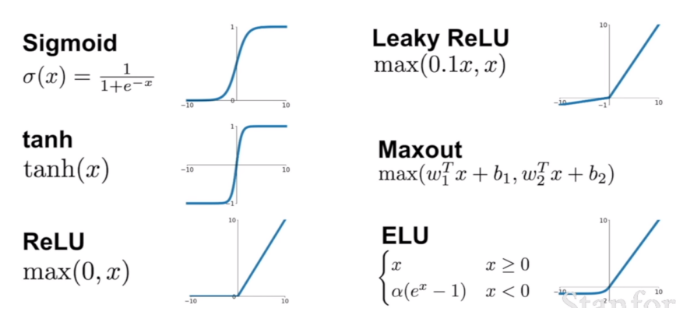
단순히 선형결합의 반복이 아닌 선형결합과 Activation Function을 통해
비선형변환을 하겠다는 것이고 그 반복이 신경망 구조를 이룬다.

Loss Function에 대해 조금 더 공부해보자.
앞에서 선형회귀를 할 때를 생각해보면 입력이 주어졌을 때
해당 출력과 Target Data 사이의 제곱을 줄이는 것이 목표였고,
이를 MSE라 했는데 이것이 늘 우리의 목표를 만족시키진 않는다.
만약 선형회귀 문제에 격차가 매우 큰 아웃라이어가 있었다고 치자.
그렇다면 MSE는 더욱 클 것이고, 이를 학습시키려다 전체적인 모델의 성능이
감소할 수 있다. 따라서 문제에 따라 손실함수를 정의하기 위해서라도
Loss Function의 특징을 보다 명확히 이해하고 있어야 한다.
분류문제에 자주 사용되는 Cross Entropy Loss에 대해 생각해보자.
일반적으로 분류 문제의 출력은 One-hot Vector로 나오기 마련이다.
y_hat을 Logit이라 하는데 우리의 목표는 모델의 출력값 중에 가장 큰 값만을
살리고 그게 곧 Label 값과 같게 만드는 것이다. 그러한 측면에서 CE 가 어떻게
분류 문제 성능을 높이는 지 고민해 볼 필요가 있다.
Why You Should Use Cross-Entropy Error Instead Of Classification Error Or Mean Squared Error For Neural Network Classifier Train
When using a neural network to perform classification and prediction, it is usually better to use cross-entropy error than classification error, and somewhat better to use cross-entropy error than …
jamesmccaffrey.wordpress.com
http://funmv2013.blogspot.com/2017/01/cross-entropy.html
분류 오차에 Cross entropy를 사용하는 이유
딥 신경망 분류 오차를 줄이기 위한 최적화는 Net 출력 결과와 사용자 Label 정보 차이를 Error 로 정의한 후, 이 값을 줄이도록 Net 파라메터를 바꾸어 나가는 것이다 . 오차로는...
funmv2013.blogspot.com
마지막 확률 모델이다. 내가 회귀모델을 풀어서 얼굴을 보고 나이를 맞추게 하겠다.
동시에 20살일 확률이 80%라거나 30살이 분명한다던가.
Gaussian 된 Log-likelihood를 Maximize 하겠다는 MLE Loss Function이다.
https://hyeongminlee.github.io/post/bnn002_mle_map/
Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP) | Hyeongmin Lee's Website
Bayes Rule을 이용한 방식의 가장 큰 단점들 중 하나는 Likelihood의 Probability Distribution을 알아야 한다는 점입니다. 물론 앞선 포스팅에서는 관찰을 통해 Likelihood를 얻었지만, 여간 귀찮은 일이 아닐
hyeongminlee.github.io